GAM method
This method belongs to the group of IDS criteria. It is a quite new criterion [GAM05]. It is based on a construction of minimum circumscribed ellipsoid over the load path in five-dimensional deviatoric Ilyushin space:
![]()
where ai correspond to length of semi-axes of the ellipsoid circumscribing the stress path in the deviatoric space. Under specific conditions – iso-frequency out-of-phase sinusoidal multiaxial loading – the following equality holds true:
![]()
where di are the distances of the centre of the ellipsoid to the faces of any arbitrarily oriented rectangular prism circumscribing the stress path in the deviatoric space [GAM05]. The final criterion utilizes the highest principal stress over the load cycle as the second load input, so that the most damaging combination could be expected:
![]()
The material variables are set from fatigue limits as:
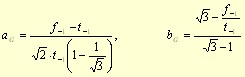
The di parameters can be set from search for minimum and maximum values of the transformed deviatoric stress tensor:
![]()
The results of the criterion reached in [FatLim Database] show problems concerning the effect of mean stress. Until now, only in the simplified version utilizing the di parameters is implemented in PragTic. Be aware of this limitation.
Nomenclature:
|
Mark |
Unit |
PragTic variable |
Meaning |
|
J2 |
[MPa] |
second invariant of stress tensor deviator |
|
|
|
[MPa] |
TENS-1, BEND-1 |
fatigue limit in fully reversed axial loading |
|
|
[MPa] |
maximum of the highest principal stress throughout the load history |
|
|
|
[MPa] |
components of the transformed deviatoric stress vector |
|
|
|
[MPa] |
TORS-1 |
fatigue limit in fully reversed torsion |
Methods & Options & Variables of Calculation – Edit
Decomposition
Elasto-plasticity
- No – currently no option implemented
Solution option
- Only every x-th data-point taken from load history
- Evaluate envelope curve only <1~yes, 0~no>
Solution variable
- Minimum damage – this option is not active for this high-cycle fatigue method
Material parameters
|
E |
[MPa] |
tensile modulus |
|
NU |
[-] |
Poisson’s ratio |
|
TENS-1 |
[MPa] |
fatigue limit in fully reversed push-pull (or plane bending) |
|
TORS-1 |
[MPa] |
fatigue limit in fully reversed torsion |
Result detail variables
Damage fatigue index is computed, not the damage as a reciprocal value to number of cycles or repetitions
FDD1 AMP_SH value of the parameter f in the first equation here
FDD2 MAX_PS maximum principal stress during loading
© PragTic, 2007
This help file has been generated by the freeware version of HelpNDoc